第十章 声源定位(DOA)

DOA(direction of arrival)，在三维空间中，除了时域、频域、还可以利用空域信息对信号进行处理，基于阵列麦克的远场语音识别场景，一些声源分离技术(beamforming, blind source seperation)会要使用到声源方位信息。声源定位技术并不仅限于单个目标源的定位，且对于ASR场景的声源目标是宽带信号。 此外，定位出声源方，还有益于产品的交互体验(寻向灯，以及电机转动姿态)。

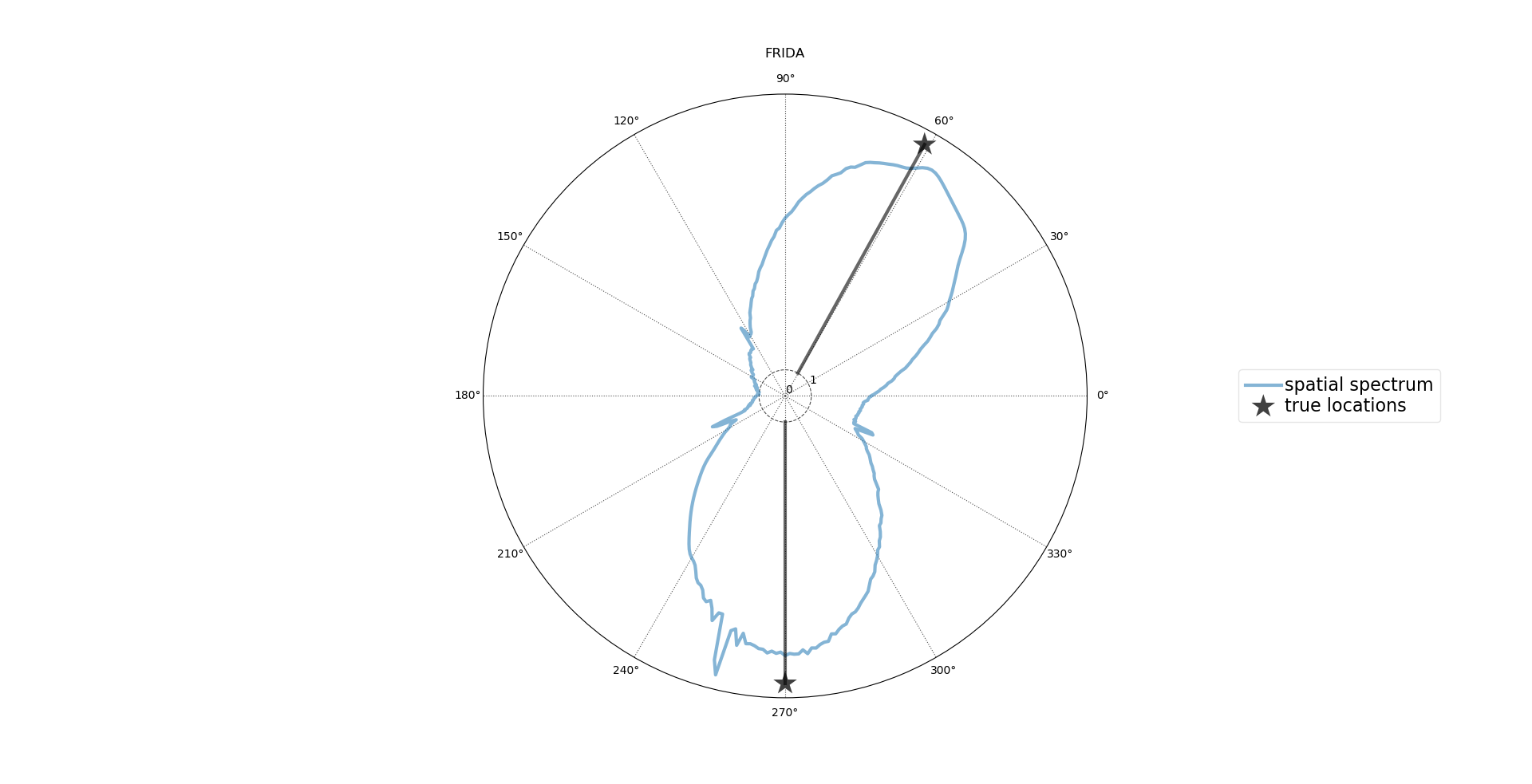
声源定位算法需要考虑鲁棒性和角分辨率两项指标。有资料表明FRIDA和MUSIC算法的鲁棒性较好，其次是SRP-PHAT和TOPS，再次WAVES和CSSM算法。在角分辨率这块FRIDA也比较好，MUSIC和SRP-PHAT次之，基于相关性的方法比非相关性方法差。

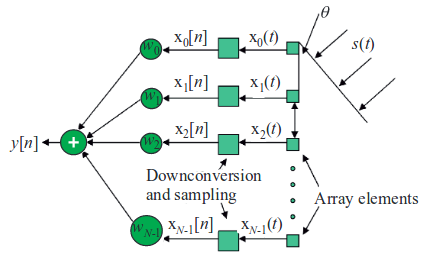
假设入射的声波是平面波，且夹角是$\theta$，则有：

$x_i(t) = s(t-\Delta_i) \tag{1}$

以第一个麦克风为参考点，则在t时刻，第k个声源到达地$n(n=1,2,\cdots, N)$麦克风的信号可表示为：

$a_ks_k(t)e^{-j(n-1)\frac{2 \pi d \sin \theta_k}{\lambda}} \tag{2}$

$a_k$是入射方向性，$a_ks_k(t)$是入射强度，对于无方向性声源，可以假设其等于1。

则第m个麦克采集到的带噪声$m$的信号可表示成下式：

$x_n(t) = \sum \limits_{k=1}^D s_k(t)e^{[-j(n-1) \frac{2 \pi d \sin \theta_k}{\lambda}]} + m_n(t) \tag{3}$

为便于表示，可以将e的指数部分用$a_n(\theta_K)$表示，则有：

$a_n(\theta_k) = e^{[-j(n-1) \frac{2 \pi d \sin \theta_k}{\lambda}]} \tag{4}$

则采集到的信号可用如下阵列表示：

$X = AS + M \tag{5}$

其中：

$X=[x_1(t), x_2(t), \cdots, x_N(t)]^T \tag{6}$

$S=[s_1(t), s_2(t), \cdots, s_D(t)]^T \tag{7}$

$A=[a(\theta_1), a(\theta_2), \cdots, a(\theta_D)]^T = \begin{equation} %开始数学环境 \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 1 & 1 & \cdots & 1\\ %第一行元素 e^{-j\phi_1} & e^{-j\phi_2} & \cdots & e^{-j\phi_D}\\ %第二行元素 \cdots & \cdots & \cdots & \cdots \\ %第一行元素 e^{-j(N-1)\phi_1} & e^{-j(N-1)\phi_2} & \cdots & e^{-j(N-1)\phi_D}\\ %第二行元素 \end{array} \right] %右括号 \end{equation} \tag{8}$

$\phi_k =\frac{ 2 \pi d }{\lambda} \sin \theta_k \tag{9}$

因为后续会有频域方法计算DOA，这里给出时间上的延迟和频域上的关系：

$s(t-\tau) \leftrightarrow S(f)e^{-j2\pi f \tau} \tag {10}$

GCC-SRP互相关技术

互相关方法具有计算量小，实时性好而被大多数系统中使用，其基于阵元之间的差异时间差(Time-Delay/Frequency-Delay)进而提取出声源距离阵元的位置信息，根据不同的麦克风对就可以在三维空间中唯一确定一个声源，互相关方法也是有缺点的，其抗噪性能差，在混响场景准确性也会降低，也有一些算法针对混响场景进行了优化，如SRP-PHAT。此外还有一些波束扫描算法，基本思想是在可能的空间点中做波束合成，然后根据合成后的各个方向上的功率最大值认为是声源方法。 两个麦克风之间的TDOA估计可以通过麦克风之间广义互相关（GCC， generalized cross-correlation）计算得到，如下两个麦克风。

$\hat \tau_{\frac {GCC}{x1x2}} = \arg \max \limits_{\tau}{\frac{GCC}{x1x2}}(\tau) \tag {11}$

这里:

${\tau}({\frac{GCC}{x1x2}}) \triangleq IFFT\{ \Psi_{x1x2}(f) \} = \int_{-\infty}^{\infty}(\Phi(f)S_{x1x2}e^{j2\pi f \tau}df \tag{12}$

其中，$\Phi(f)$是频域权重函数，$S_{x1x2}(f)$是互相关的频域计算。

$S_{x1x2} \triangleq E[X_1(f)X_2*(f)] \tag {13}$

频域权重函数$\Phi(f)$对延迟估计的影响较大。

• 经典互相关法 理想远场模型$\Phi(f) =1$
• 平滑互相关变换(SCOT, smoothed coherence transform)

$\Phi(f) = - \frac{1}{\sqrt{E\{ |X_1(f)|^2|X_2(f)|^2\}}} \tag {14}$

$X_n(f) = \sum \limits_k x_n(k)e{-j2\pi k}, n=1,2,\cdots \tag {15}$

这里推导一下SCOT适应场景:

$\begin{multline} \Psi_{\frac{SCOT}{x_1x_2}} (f)= \frac{\alpha_1\alpha_2 e^{-j2\pi f \tau_{12}}E\{ |S(f)|^2\}}{\sqrt{E[ |X_1(f)|^2 E|X_2(f)|^2}}\\ = \frac{\alpha_1 \alpha_2 e^{-j2\pi f \tau_{12}}E|S(f)|^2}{\sqrt{\alpha_1^2E|S(f)|^2 +\sigma_{b_1}^2(f)}} \times \frac{1}{\sqrt{\alpha_2^2E|S(f)|^2+ \sigma_{b_2}^2(f)}} \\ =\frac{e^{-j2\pi f \tau_{12}}}{\sqrt{1+\frac{1}{SNR_1(f)}}\cdot \sqrt{1+\frac{1}{SNR_2(f)}}} \end{multline} \tag{16}$

假设两个麦克风采集到的信息的信噪比相等，则有:

$\Psi_{\frac{SCOT}{x_1x_2}}(f) = \frac{SNR(f)}{1+SNR(f)} \times e^{-j2\pi f \tau_{12}} \tag{17}$

从上式可以看出,计算的准确性适用于信噪比较高的场合,但是对于高混响场景来说效果就不行,实际效果也确实是这样.

• 相位变换法 权重变成由相位组成而不是互功率谱幅度。

$\Phi(f) = \frac{1}{S_{x_1x_2}(f)} \tag{18}$

由此可得$\Psi_{\frac{PHAT}{x_1x_2}}(f) = e^{-j2\pi f \tau_{12}}$,这和SCOT在SNR趋于无穷大时结果一致. GCC算法在适度噪声和无混响环境下较好,且计算量小,跟踪实时性好,对于混响,需要采用倒谱滤波器以滤除混响的影响.

在工程实现上时域卷积等于频域相乘,在频域里进行计算以减小计算量,且在对频点的处理上,声源发声所在的频点能量较高,可以选择一部分频点以减少无关频点的扰动影响.

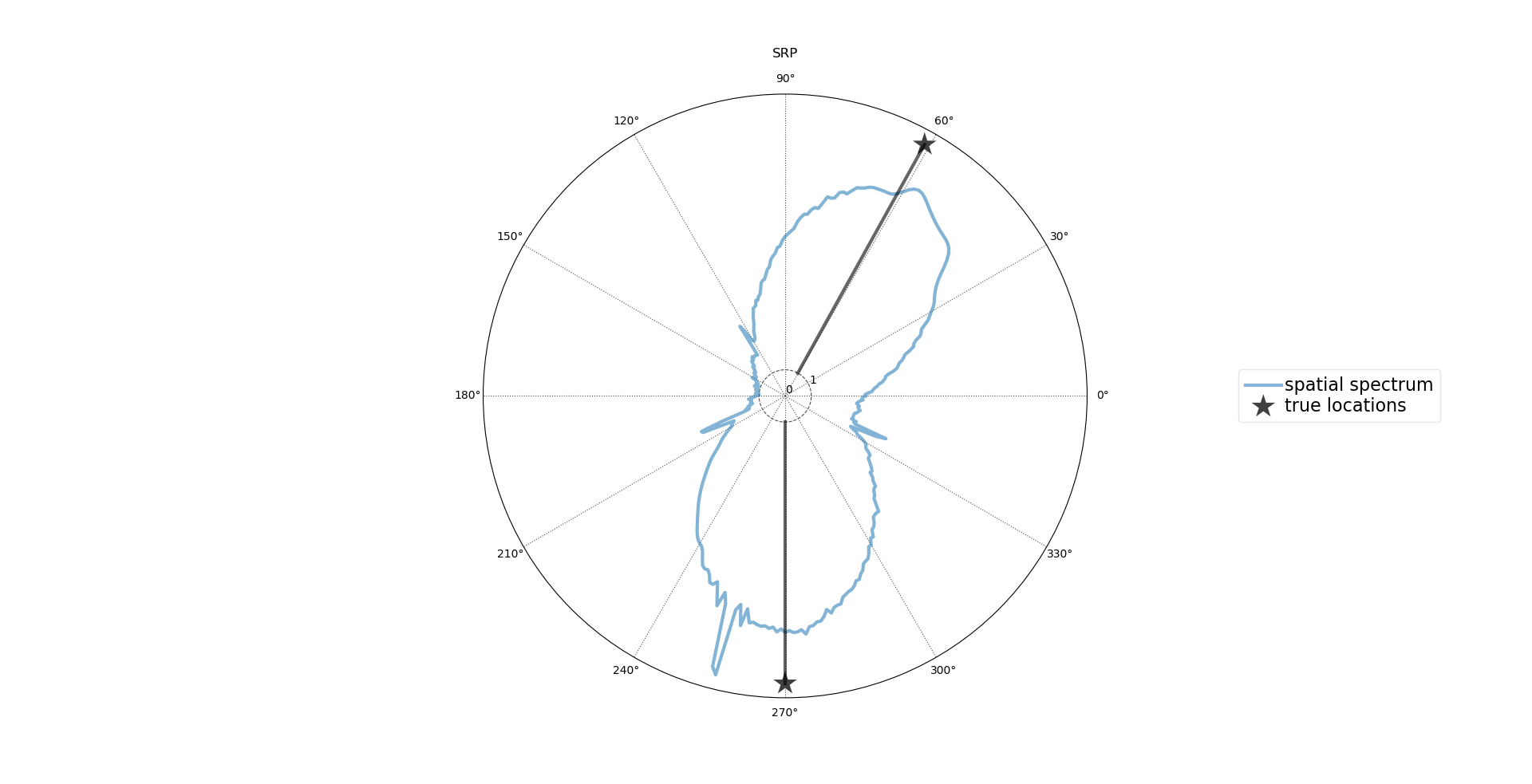
MUSIC算法

MUSIC算法（MUsical Signal Classification）基于子空间法，MUSIC方法具有分辨率高的特性。用到二阶统计量信息，根据式5采集到的信号，得协方差矩阵可表示为：

$R_x=E[XX^H] \tag{19}$

$H$是转置共轭运算符。假设信号和噪声是不相关的，则式5带入式19可得下式：

$R_x=E[(AS+M)(AS+M)^H] = AE[SS^H]A^H + E[MM^H] = AR_sA^H + R_M \tag{20}$

其中$R_s=E[SS^H]$是声源信号自相关矩阵，假设噪声之间是不相关的，则噪声的协方差矩阵退化成如下的单位阵：

$R_M= \delta^2I \tag{21}$

在实际应用中，无法精确得到$R_x$,采用近似的方法获得：

$\hat R_x= \frac{1}{N} \sum \limits_{i=1}^N x(i)x^H(i) \tag{22}$

$\hat R_x$是$R_x$的最大似然估计，当$N \rightarrow \infty$估计值无线逼近真实值。

$R_x = AR_sA^H + \sigma^2I \tag{23}$

由于$\sigma^2 \gt 0$，$R_x$是一个满秩矩阵，其有N个正实数特征值$\lambda_1, \lambda_2, \cdots, \lambda_N$，对应的有N个特征向量$v_1, v_2, \cdots, v_N$，又因为$R_x$是艾米尔特矩阵，则特征向量是正交的：

$v_i^Hv_j = 0 \quad i \ne j \tag{24}$

特征值按照降序排列如下：

$\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_N \gt 0 \tag{25}$

25式中靠前的D个特征值对应于信号，剩下的N-D个特征值对应于噪声。

特征和特征向量满足下式：

$R_x V_i = \lambda_i V_i \tag{26}$

另$\lambda_i= \sigma^2$是最小特征值，则有：

$R_xV_i = \sigma^2 V_i \quad i=D+1,D+2, \cdots, N \tag{27}$

将23带入27得：

$\sigma^2 V_i = (AR_sA^H+\sigma^2I)V_i \tag{28}$

则可以得到：

$AR_sA^HV_i = 0 \tag{29}$

因为$A^HA$是DXD的满秩矩阵，则逆矩阵是存在的，则29两边同乘以$R_s^{-1}(A^HA)^{-1}A^HAR_sA^HV_i = 0 \tag{30}$

则进一步可得：

$A^HV_i = 0 \quad i=D+1,D+2, \cdots, N \tag{31}$

31表明，噪声的特征向量是和A列正交的，A的每一行是信号的一个方向。MUSIC思想就是用噪声的特征向量计算生源的方位。

噪声矩阵构建如下：

$E_m = [V_{D+1}, V_{D+2}, \cdots, V_{N}] \tag{32}$

根据噪声矩阵，可以得到空间谱$P_{mu}(\theta)$:

$P_{mu}(\theta) = \frac{1}{a^H(\theta)E_mE_m^H a(\theta)} = \frac{1}{||E_m^Ha(\theta)||^2} \tag{33}$

MUSIC算法流程是： 首先估计采集信号的特征矩阵：

$R_x = \frac{1}{N} \sum \limits_{i=1}^NX(i)X^H(i) \tag{34}$

进行特征值分解得到：

$R_x = AR_sA^H + \sigma^2I \tag{35}$

根据特征值的顺序，根据目标数D，得到噪声矩阵$E_m$:

$A^Hv_i = 0 \quad i=D+1, D+2, \cdots, N \tag{36}$

$E_m= [V_{D+1}, V_{D+2}, \cdots, V_{D+3} \tag{37}$

变换$\theta$，根据33计算空间谱能量，能量峰值所在位置即为目标声源的方向。

对MUSIC算法的改进和实现，有root-MUSIC。

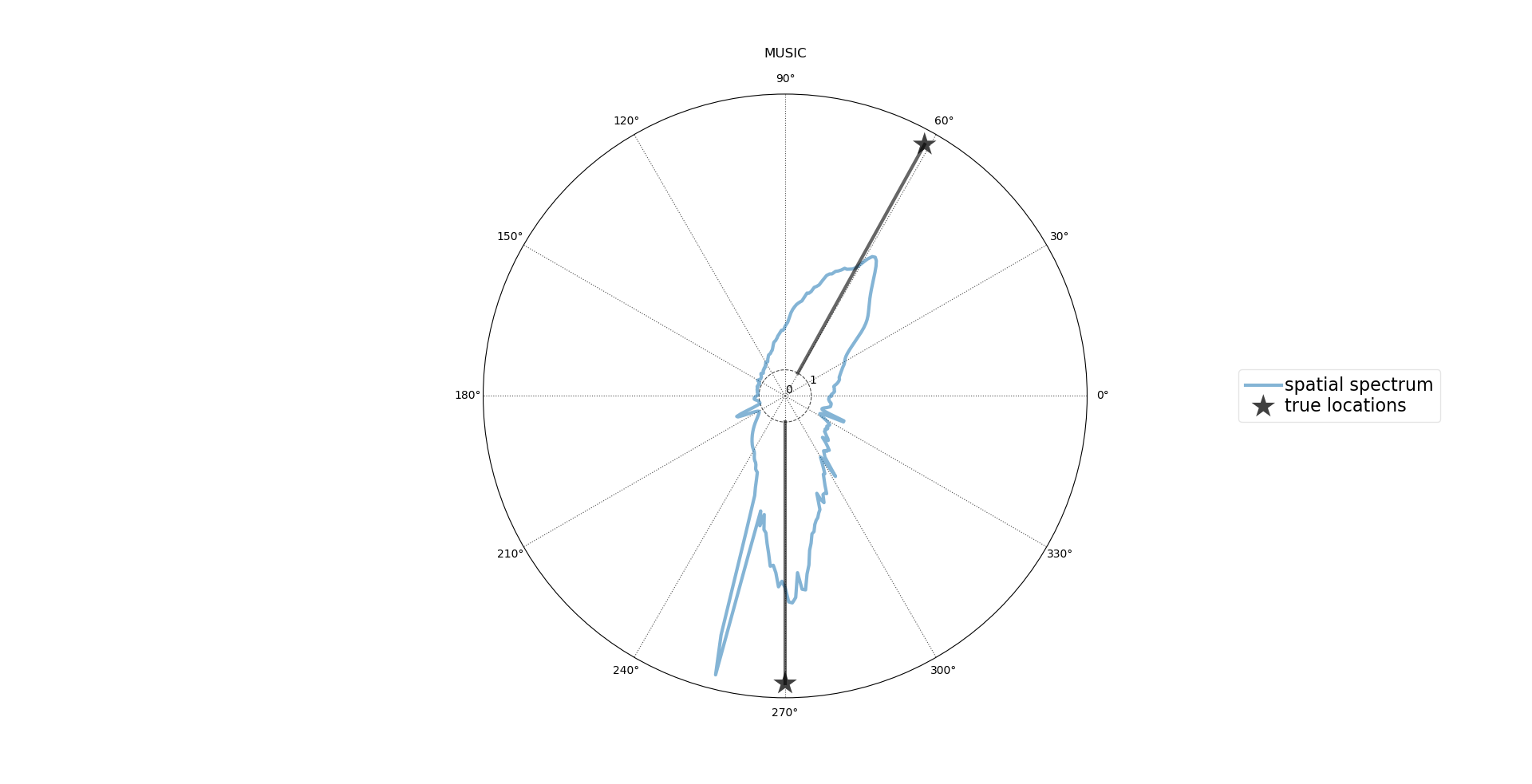
TOPS算法

test of orthogonality of projected subspaces。该方法通过信号和噪声子空间多个频率成分的正交关系估计声源方位，TOPS可用于一维和二维阵列，和CSSM(coherent signal subspace method)及WAVES之列宽带相关方法不同，该方法不需要对初始信号预处理，基于互相关的方法在低信号比时可以获得较好的效果，非互相关的方法在高信噪比可以获得比较好的效果，TOPS在SNR处在中等范围是可以或获得较好的效果。

大多数宽带子空间方法通过滤波器组或者DFT的方法将信号分解为多个子带信号.根据图1和式子1，用DFT方法将信号变换到频域得到：

$\mathbf X_m(\omega)= \sum \limits_{l=0}^{D-1}S_l(\omega)e^{-j\omega \Delta_l} + M_n(\omega) \tag{38}$

如果选定的频率范围是$[\omega_L, \omega_H]$，则DFT的结果对应于选定K个bin值，则可以表示成下式：

$\mathbf X(\omega_i) = \mathbf A(\omega_i,\mathbf \theta) \mathbf S(\omega_i) + \mathbf M(\omega_i), i=0,1,\cdots, K-1. \tag{39}$

其中：

$\mathbf X(\omega_i) = \begin{equation} %开始数学环境 \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 X_0(\omega_i) & X_1(\omega_i) & \cdots & X_{N-1}(\omega_i)\\ %第一行元素 \end{array} \right]^T %右括号 \end{equation} \tag{40}$

$\mathbf S(\omega_i) = \begin{equation} %开始数学环境 \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 S_0(\omega_i) & S_1(\omega_i) & \cdots & S_{N-1}(\omega_i)\\ %第一行元素 \end{array} \right]^T %右括号 \end{equation} \tag{41}$

$\omega_L \le \omega_i \le \omega_H, \forall i$，$A(\omega_i, \mathbf \theta)$是$N\times D$的方向向量，D是声源个数，N是麦克风阵列数量。

$\mathbf A(\omega_i, \mathbf \tau_d) = \begin{equation} %开始数学环境 \left[ %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 \mathbf a_0(\omega_i, \tau_0) & \mathbf a_1(\omega_i, \tau_1) & \cdots & \mathbf a_{N-1}(\omega_i, \tau_{D-1})\\ %第一行元素 \end{array} \right]^T %右括号 \end{equation} \tag{42}$

式42的每一列都是$N \times 1$维，在频率为$\omega_i$时对应的主瓣是$\mathbf a(\omega_i, \tau_l)$:

$\mathbf a(\omega_i, \tau_d) = \begin{equation} \left[ \begin{array}{ccc} 1e^{-j\omega_i\tau_{d1}} & \cdots & e^{-j\omega_i\tau_{dN}} \end{array} \right]^T \end{equation} \tag{43}$

d是声源的索引，为了后面公式简单，忽略频率，将$\mathbf A(\omega_i, \mathbf \tau)$写作$\mathbf A(\mathbf \tau)$，同理，$\mathbf a_i(\omega_i, \tau_j)$写为$\mathbf a_j(\tau_j)$。

假设D个信号是不相关的，则根据式子19和20，$\mathbf R_s$是满秩矩阵，则信号子空间矩阵和噪声子空间矩阵可以表示如下：

$\mathbf F_i = \begin{equation} \left[ \begin{array}{ccc} \mathbf y_{i,1} & \mathbf y_{i,2} & \cdots & \mathbf y_{i,D} \end{array} \right]^T \end{equation} \tag{44}$

$\mathbf W_i = \begin{equation} \left[ \begin{array}{ccc} \mathbf y_{i,D+1} & \mathbf y_{i,D+2} & \cdots & \mathbf y_{i,N} \end{array} \right]^T \end{equation} \tag{45}$

$y_{i,1}, y_{i,2},\cdots, y_{i,N}$是采集到信号协方差矩阵$R_i$的特征值按降序排序对应的特征向量。

TOPS使用对角酉变换矩阵，变换阵$\mathbf \Phi(\omega_i, \tau_i)$的第k个对角元素表示如下：

$[\mathbf \Phi(\omega_i,\tau_i)]_{(k,k)} = e^{-j\omega_i \tau_i} \tag{46}$

变换矩阵可以保持主瓣不变。

令$\Delta \omega=\omega_j -\omega_i$，在$\mathbf {\hat \theta}$和$\phi$满足如下关系时：

$[\hat {\mathbf \theta}]_i = arcsin\{\frac{\omega_i}{\omega_j}\sin \theta_i + \frac{\Delta \omega}{\omega_j}\sin \phi\} \tag{47}$

有下面两个距离空间是等价的：

$\mathscr{R}\{\mathbf \Phi(\Delta \omega, \phi)\mathbf F_i\} = \mathscr{R}\{\mathbf A(\omega_i,\mathbf {\hat \theta})\} \tag{48}$

当$2D \le N$和$K \ge D+1$时，可以将$N \times D$为的矩阵$\mathbf U_i(\phi)$定义如下：

$\mathbf U_i(\phi) = \mathbf \Phi(\Delta\omega_i, \phi) \mathbf F_0, \quad i=1,\cdots, K-1 \tag{49}$

$\Delta \omega_i = \omega_i - \omega_0$，$\phi$是假设的方位角。定义TOPS矩阵$D \times (K-1)(N-D)$的矩阵$\mathbf D(\phi)$如下：

$\mathbf D(\phi) = [\mathbf U_1^H \mathbf W_1|\mathbf U_2^H \mathbf W_2|\cdots|\mathbf U_{K-1}^H \mathbf W_{K-1}] \tag{50}$

由于真实的互相关矩阵是无法获得的，使用子空间投影法可以减少对其估计的误差，定义零空间$\mathbf a_i(\phi)$的投影矩阵$\mathbf P_i(\theta)$:

$\mathbf P_i(\phi) = \mathbf I - (\mathbf a_i^H(\phi) \mathbf a_i(\phi))^{-1}\mathbf a_i(\phi) \mathbf a_i^H(\phi) \tag{51}$

则通过下式可以得到修正后的TOPS矩阵$\mathbf D(\phi)$：

$\mathbf U_i^{'}(\phi) = \mathbf P_i(\phi) \mathbf U_i(\phi) \tag {52}$

这可以减少噪声子空间中泄漏的信号子空间成分。

TOPS算法的步骤如下： 1.将麦克风采集到的信号分成J个块； 2.计算J个块的DFT； 3.对于第j个块，在预选的$\omega_k$上选择$X_{j,k}$;$k=0,\cdots,K-1, j=0,\cdots, J-1$ 4.根据估计的协方差矩阵$\mathbf {\hat R_k}$,用奇异值SVD分解法计算信号子空间$\mathbf {\hat F}_1$和噪声子空间$\mathbf {\hat W_k}$，$k=1,\cdots,K-1$ 5.对于假设的方向$\phi$，使用58和50计算$\mathbf {\hat D}(\phi)$ 6.通过下式准则估计得到$\hat \theta$。

$\hat \theta = \arg \mathop{max}\limits_{\phi} \frac{1}{\sigma_{min}(\phi)} \tag{53}$

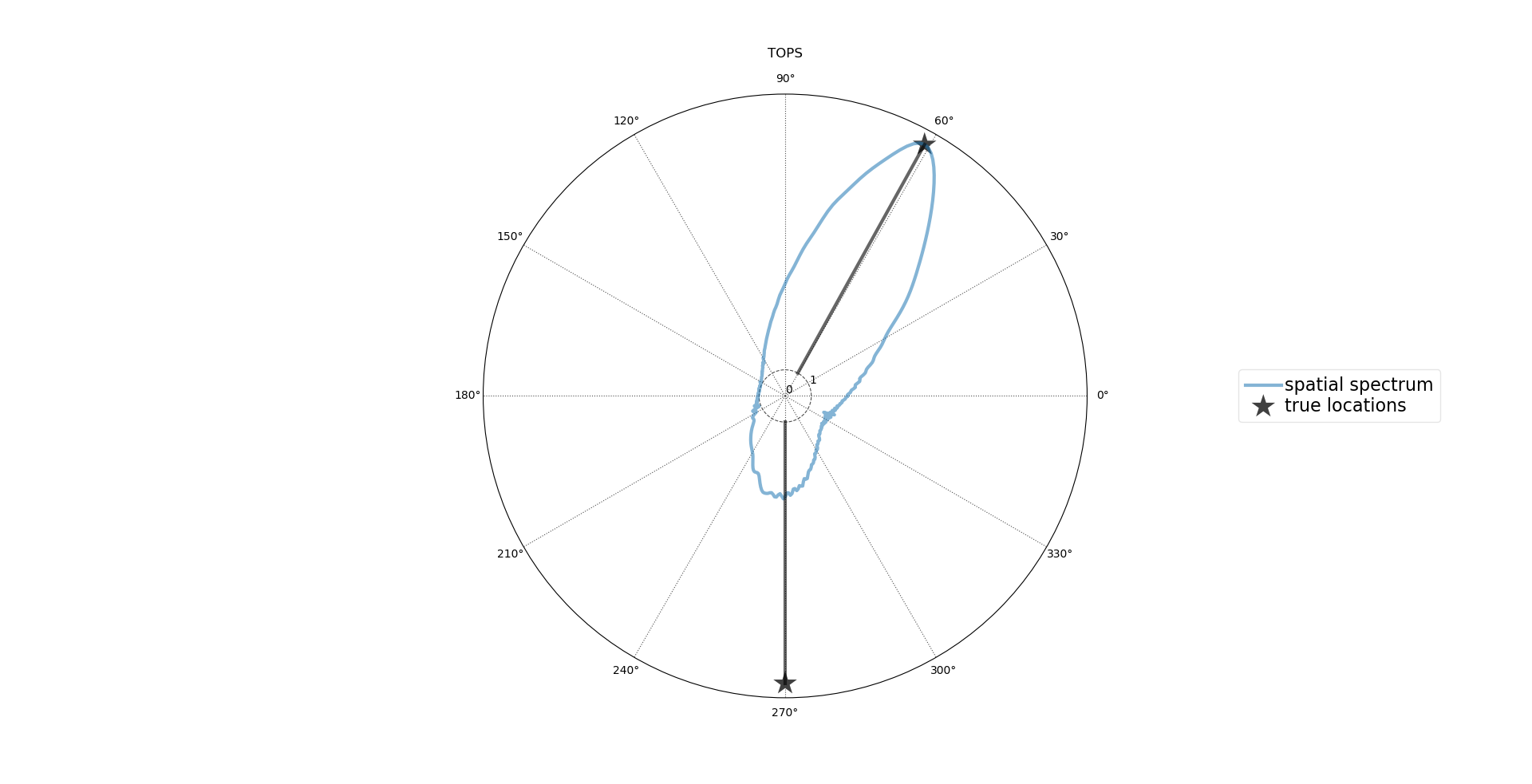
FRIDA算法

FRI(finite rate of innovation sampling based algorithm)，该算法实现的方法已经开源了，源码点击