第二十三章 高斯分布和EM算法

在做ASR识别的声学模型时,用到多维高斯模型和EM算法,在做CGMM的波束形成时也用到了高斯分布和EM算法。

马氏距离

如图二给出的两个列表,$m_1(x_1,y_2),m_2(x_2,y_2)$,$x_1,y_1$是第一个类别两个维度的中心距的坐标，对于一个新给的变量X，判断其所属的类别可以使用最近临域边界法,即求x分别到两个类别中心的距离，里哪个类别距离小，就可以将其归为哪个类别。可以更进一步，将距离通过指数函数$e^{-||x-m||}$转换成概率，增加权重因子$c$可得$e^{- \frac{||x-m||}{c}}$。

对于多维情况,指数部分求距离则变成${(\mathbf x -\mathbf m)^T\mathbf \Sigma^{-1}(\mathbf x -\mathbf m)}$。这个距离被称为马氏距离。

协方差矩阵的种类

球形,对角和全协方差矩阵

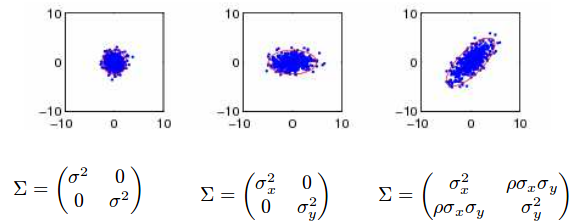
高斯分布

高斯分布(Gaussian distribution)又称为正太分布(Normal distribution).

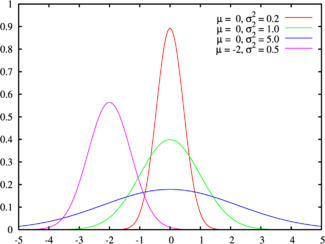
一维高斯分布

若随机变量$x$服从均值为$\mu$,标准方差为$\sigma^2$的高斯分布,则记为: $X \sim N(\mu, \sigma^2) \tag {1}$ 其概率密度函数记为: $f(x;\mu, \sigma)= \frac{1}{\sigma\sqrt{2\pi}}\exp(-\frac{(x-\mu)^2}{2\sigma^2})$

二维高斯分布

二维随机变量的高斯分布如下: $f(x,y)=\frac{1}{2\pi \sigma_x \sigma_y \sqrt{1-\rho^2}} \exp (- \frac{1}{2(1-\rho^2)}[\frac{(x-\mu_x)^2}{\sigma_x^2} + \frac{(y-\mu_y)^2}{\sigma_y^2}- \frac{2\rho(x-\mu_x)(y-\mu_y)}{\sigma_x \sigma_y}] ) \tag{2}$ 其中$\rho$是$x$和$y$之间的相关系数, 在$\sigma_x > 0$且$\sigma_y > 0$的情况下,可以令:

$$\mathbf{ \mu} = \begin{bmatrix} x\\ y \end{bmatrix}, \mathbf \Sigma =\begin{bmatrix} \sigma_x^2 && \rho \sigma_x \sigma_y\\ \rho \sigma_x\sigma_y && \sigma_y^2 \end{bmatrix}$$

则有: $f_x(x, y) = \frac{1}{\sqrt{(2\pi)^2|\mathbf \Sigma|}}\exp(-\frac{1}{2}( \begin{bmatrix} x - \mu_x \\ y - \mu_y \end{bmatrix}^T \mathbf \Sigma^{-1}\begin{bmatrix} x - \mu_x \\ y - \mu_y \end{bmatrix})\tag {3}$

通过求解$| \mathbf \Sigma|$行列式的值,和二维矩阵求逆$\mathbf \Sigma^{-1}$计算公式是:

$$\begin{bmatrix} a && b\\ c && d \end{bmatrix}^{-1} = \frac{1}{ad-bc}\begin{bmatrix} d && -b\\ -c && a \end{bmatrix}=\frac{1}{\sigma_x^2\sigma_y^2 - \rho^2 \sigma_x^2\sigma_y^2}\begin{bmatrix} \sigma_y^2 && -\rho\sigma_x \sigma_y\\ -\rho \sigma_x^2\sigma_y^2 && \sigma_x^2 \end{bmatrix} \tag{4}$$

对角阵 假设上述变量$x$和$y$是不相关的,那么其相关系数$\rho=0$,则协方差矩阵变为: $\mathbf \Sigma=\begin{bmatrix} \sigma_x^2 && 0\\ 0 && \sigma_y^2 \end{bmatrix}$

在有些场景中,为了减少运算量,假设建模的对象(如语言发音模型)分类是不相关的,则由协方差矩阵蜕化为对角阵,kaldi中就有对角高斯混合模型协方差矩阵类型可选.

多维高斯分布

对于语音识别中的声学模型,每段语音分帧提取MFCC特征多半是40维度,或者NN方法中的fbank也多半选择了40维.将上节的二维拓展到多维分布后可得如下概率密度函数: $f_{\mathbf X}(x_1,\cdots, x_k) = \frac{1}{\sqrt{(2\pi)^k|\mathbf \Sigma|}}\exp(-\frac{1}{2}(\mathbf x -\mathbf \mu)^T\mathbf \Sigma^{-1}(\mathbf x -\mathbf \mu)) \tag{5}$

此外还有复高斯模型,其每一维变量都包括实部和虚部.

EM算法

一维高斯分布的EM算法

EM算法的初始化:

• 设置随机变量集$\mathbf X = \{x_1, \cdots, x_N\}$的初始均值估计$\hat \mu_1, \cdots, \hat \mu_k$,如K=3(类别), N=100,即100个随机变量分类到三个类别中去, 则可以设置$\hat \mu_1 = x_{45}, \hat \mu_2 = x_{32}, \hat \mu_2 = x_{10}$.
• 计算初始协方差参数,$\hat \sigma_1^2, \cdots, \hat \sigma_k^2 = \frac{1}{N}\sum_{i=1}^N(x_1 - \overline x )^2, \overline x = \frac{1}{N}\sum_{i=1}^Nx_i$
• 设置随机变量的初始分布为均匀分布: $\hat \phi_1, ..., \hat \phi_K = \frac{1}{K}$.

E步骤:

• 对$\forall i, k$计算 $\hat \gamma_{ik} = \frac{\hat \phi_kN(x_i|\hat \mu_k, \hat \sigma_k)}{\sum_{j=1}^K \hat \phi_j N(x_i|\hat \mu_j, \hat \sigma_j)} \tag {6}$ 此处$\hat \gamma_{ik}$是$x_i$属于类别$C_K$的概率,即$\hat \gamma_{ik} = p(C_k|x_i, \hat \phi, \hat \mu, \hat \sigma)$.

M步骤: 使用E步骤计算的$\hat \gamma_{ik}$对$\forall k$计算:

• $\hat \phi_k =\sum \limits_{i=1}^N \frac{\hat \gamma_{ik}}{N}$
• $\hat \mu_k= \frac{\sum_{i=1}^N \hat \gamma_{ik} x_i}{\sum_{i=1}^N \hat \gamma_{ik}}$
• $\hat \sigma_k = \frac{\sum_{i=1}^N \hat \gamma_{ik}(x_i - \hat \mu_k)^2}{\sum_{i=1}^N \hat \gamma_{ik}}$

收敛结束条件:

• 一种是按找EM总数算,一种是按照M步骤连续两次的目标值差异度算.

聚类操作,是指并不知道参数的类别总数时将相近的随机变量合并成同一个类.

高斯混合模型c代码下载链接