MVDR算法改进
MVDR算法公式中要用到矩阵求逆,这在工程实现中很难实时处理,所以采用了迭代和变换模型的方式避免矩阵求逆运算,另外MVDR算法对和波束同方向的噪声是无能为力的,虽然前文中单路可以实现降噪功能,但是基于阵列的多麦克场景可以使用更多的麦克风空间信息,本文基于改进了当前一些消除同方向噪声的方法,得到了很好的效果。
后置滤波Post-filtering
使用麦克风阵列,根据空域选择性,可以抑制波束指向之外的噪声,干扰,对于和波束指向同方向的噪声则使用后置滤波的方法进行消除。后置滤波主要通过估计语音、噪声以及干扰的功率谱密度来对波束的结果进一步处理,以降低噪声和干扰。估计出这些功率谱密度后,然后对波束形成(DAS,LCMV,Filter-sum,MVDR)后的结果按功率谱情况再加一次增益处理,这个处理主要是用于抑制同方向的噪声,干扰。 在实时处理时语音,噪声以及干扰的功率谱密度并不容易准确的估计得到。一些论文里阐述了如何获得这些功率谱密度估计。
本文主要介绍如下方法:
1) mvdr without postfilter 2) mvdr + zelinski postfilter 3) mvdr + mccowan postfilter 4) mvdr + lefkim postfilter 5) mvdr + stsa postfilter 6) mvdr + log-stsa postfilter
维纳滤波
使用最小均方误差准则
其中:
式2对求偏导数后可得:
,,
这种方法不需要方向向量,但是依赖输入信号和目标信号,当应用场景确定时,可以预先根据传输信号和目标信号,训练得到
最小失真(MVDR)
使用朗格朗日乘子法求解得到:
MVDR参考[Superdirective+Microphone+Arrays.pdf]
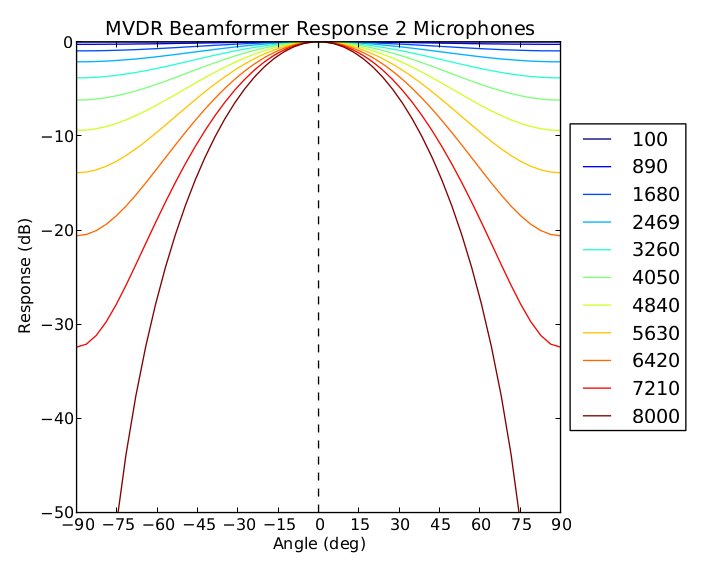
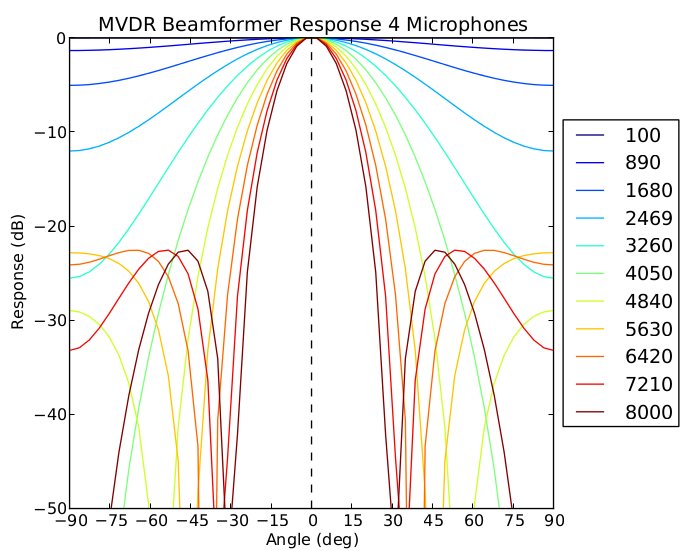
最大信号干扰比
和式5类似,可得:
Zelinski后置滤波
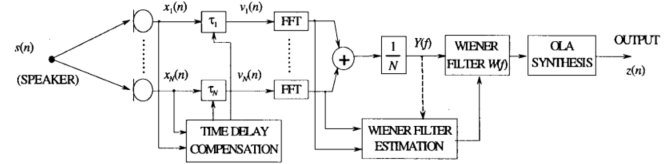
该算法的主要作用是抑制不相关的散射噪声,首先对信号进行传播延迟补偿,得到,延迟补偿模块的做法是根据声源位置,计算到达各个麦克风的时间差,这样计算得到每个麦克风对语音频带内各个频点的补偿值,然后对的一帧10ms,或者20ms做FFT变换,在频域补偿各个频点后再变换到时域得到。然后经过一个维纳滤波后处理,则其最优权重如下式:
是delay-sum输出值,是信号和波束结果的互功率谱,而是波束结果的自功率谱。
又假设噪声是不相关的,则,则7可以变为下式:
对于MVDR方法,将delay-sum的权重调整和后置滤波合二为一,则权重变为:
那么问题变为求解:
当如下假设成立时:
1.噪声和信号不相关, 2.噪声功率谱比较小时, 3.噪声是不相关的;
那么可得如下简化:
可以使用迭代的方式求解互功率谱:
其中是接近单位1的值,,D是滤波器组抽取因子。
可以根据估计,使用平均的方法进一步提高估计的准确性,这样可以得到
Zelinski算法假设不同麦克风采集到的信号是完全不相关的,也就是麦克风采集到的信号是统计独立不相干的,在低频和麦克风间距较近时,这一假设并不成立,该后置滤波并不是最优的,导致相干的噪声无法消除,低频的相干性强,导致无法消除。另外,该算法导致了语音的失真。
mccowan后置滤波
当不同麦克风的噪声存在相关性时,它们的相关性可定义如下:
相关性的值.
假设噪声符合各向同性散射声场模型场景,如办公室,汽车,它们的相关性可用sinc或者零阶贝塞尔函数来表示:
zelinski假设,这完全忽视了通道间采集到的噪声的相关性。如果考虑相关性,则功率谱如下:
如果,则17~19可简化为如下:
根据21~23信号功率谱可以按如下计算:
将上式子带入14可以计算得到mccowan的后滤波权重:
lefkim
S. Lefkimmiatis, D. Dimitriadis, and P. Maragos, “An optimum microphone array post-filter for speech applications.,” in Proc. Interspeech Conf. , 2006.